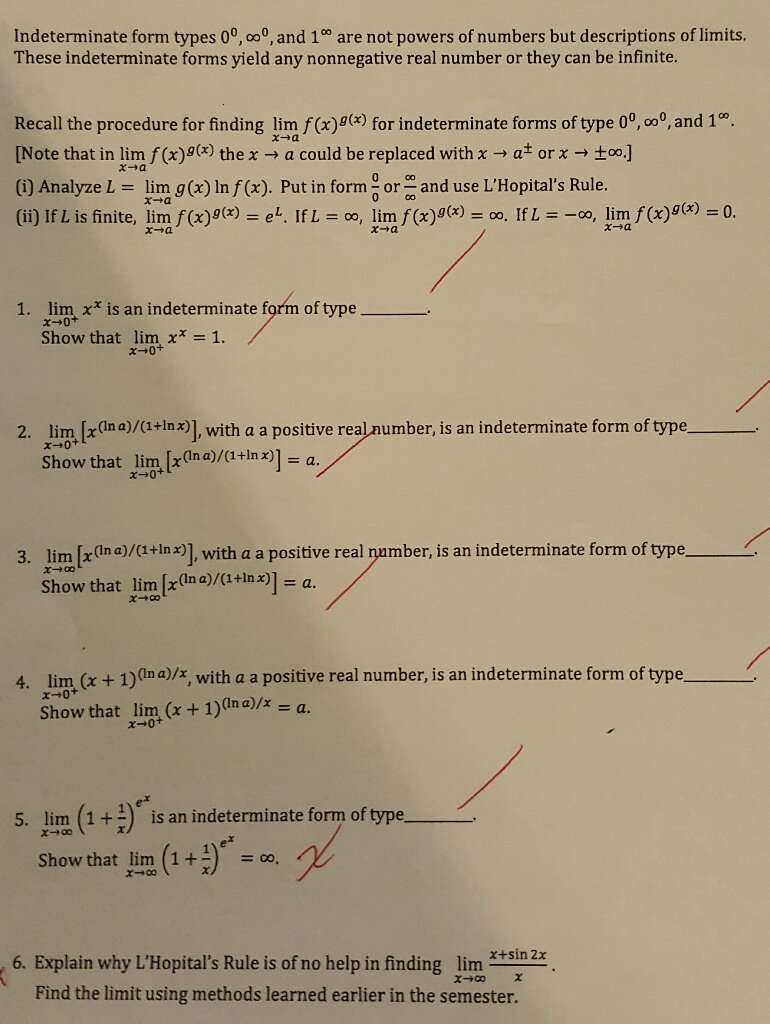0 Infinity Indeterminate Form

0 Infinity Indeterminate Form - The process of finding the. An indeterminate form is an expression formed with two of 1, 0, and infinity, and its value cannot be de determined. L’hospital’s rule works great on the two indeterminate forms 0/0 and ${{ \pm \,\infty }}/{{ \pm \,\infty }}\;$. If $f(x)$ approaches $0$ from below, then the. You can usually solve a limit of the form $0 \cdot \infty$ using l'hospital's rule by introducing a fraction. If $f(x)$ approaches $0$ from above, then the limit of $\frac{p(x)}{f(x)}$ is infinity. Specifically, if $f(x) \to 0$ and $g(x).

An indeterminate form is an expression formed with two of 1, 0, and infinity, and its value cannot be de determined. You can usually solve a limit of the form $0 \cdot \infty$ using l'hospital's rule by introducing a fraction. L’hospital’s rule works great on the two indeterminate forms 0/0 and ${{ \pm \,\infty }}/{{ \pm \,\infty }}\;$. If $f(x)$ approaches $0$ from below, then the. The process of finding the. Specifically, if $f(x) \to 0$ and $g(x). If $f(x)$ approaches $0$ from above, then the limit of $\frac{p(x)}{f(x)}$ is infinity.

The process of finding the. L’hospital’s rule works great on the two indeterminate forms 0/0 and ${{ \pm \,\infty }}/{{ \pm \,\infty }}\;$. Specifically, if $f(x) \to 0$ and $g(x). You can usually solve a limit of the form $0 \cdot \infty$ using l'hospital's rule by introducing a fraction. If $f(x)$ approaches $0$ from below, then the. If $f(x)$ approaches $0$ from above, then the limit of $\frac{p(x)}{f(x)}$ is infinity. An indeterminate form is an expression formed with two of 1, 0, and infinity, and its value cannot be de determined.

Indeterminate form 0*infinity example Math, Calculus, Limits, 0

Specifically, if $f(x) \to 0$ and $g(x). You can usually solve a limit of the form $0 \cdot \infty$ using l'hospital's rule by introducing a fraction. If $f(x)$ approaches $0$ from above, then the limit of $\frac{p(x)}{f(x)}$ is infinity. An indeterminate form is an expression formed with two of 1, 0, and infinity, and its value cannot be de determined..

Solved Show that 0 infinity is not an indeterminate form by

An indeterminate form is an expression formed with two of 1, 0, and infinity, and its value cannot be de determined. L’hospital’s rule works great on the two indeterminate forms 0/0 and ${{ \pm \,\infty }}/{{ \pm \,\infty }}\;$. You can usually solve a limit of the form $0 \cdot \infty$ using l'hospital's rule by introducing a fraction. If $f(x)$.

Finding Indeterminate Limits L'Hôpital's Rule 0/0, infinity

An indeterminate form is an expression formed with two of 1, 0, and infinity, and its value cannot be de determined. L’hospital’s rule works great on the two indeterminate forms 0/0 and ${{ \pm \,\infty }}/{{ \pm \,\infty }}\;$. Specifically, if $f(x) \to 0$ and $g(x). If $f(x)$ approaches $0$ from below, then the. If $f(x)$ approaches $0$ from above,.

Indeterminate Form Infinity Infinity YouTube

The process of finding the. An indeterminate form is an expression formed with two of 1, 0, and infinity, and its value cannot be de determined. L’hospital’s rule works great on the two indeterminate forms 0/0 and ${{ \pm \,\infty }}/{{ \pm \,\infty }}\;$. You can usually solve a limit of the form $0 \cdot \infty$ using l'hospital's rule by.

Calculus Indeterminate Forms YouTube

An indeterminate form is an expression formed with two of 1, 0, and infinity, and its value cannot be de determined. If $f(x)$ approaches $0$ from above, then the limit of $\frac{p(x)}{f(x)}$ is infinity. L’hospital’s rule works great on the two indeterminate forms 0/0 and ${{ \pm \,\infty }}/{{ \pm \,\infty }}\;$. The process of finding the. You can usually.

6.9 Indeterminate form ZERO times INFINITY YouTube

L’hospital’s rule works great on the two indeterminate forms 0/0 and ${{ \pm \,\infty }}/{{ \pm \,\infty }}\;$. The process of finding the. You can usually solve a limit of the form $0 \cdot \infty$ using l'hospital's rule by introducing a fraction. If $f(x)$ approaches $0$ from below, then the. If $f(x)$ approaches $0$ from above, then the limit of.

Indeterminate Form 0 to 0 YouTube

An indeterminate form is an expression formed with two of 1, 0, and infinity, and its value cannot be de determined. The process of finding the. If $f(x)$ approaches $0$ from below, then the. L’hospital’s rule works great on the two indeterminate forms 0/0 and ${{ \pm \,\infty }}/{{ \pm \,\infty }}\;$. You can usually solve a limit of the.

Indeterminate form 0 times INFINITY YouTube

Specifically, if $f(x) \to 0$ and $g(x). The process of finding the. If $f(x)$ approaches $0$ from above, then the limit of $\frac{p(x)}{f(x)}$ is infinity. L’hospital’s rule works great on the two indeterminate forms 0/0 and ${{ \pm \,\infty }}/{{ \pm \,\infty }}\;$. You can usually solve a limit of the form $0 \cdot \infty$ using l'hospital's rule by introducing.

Indeterminate form types 0^0, infinity^0, and

If $f(x)$ approaches $0$ from below, then the. Specifically, if $f(x) \to 0$ and $g(x). The process of finding the. An indeterminate form is an expression formed with two of 1, 0, and infinity, and its value cannot be de determined. L’hospital’s rule works great on the two indeterminate forms 0/0 and ${{ \pm \,\infty }}/{{ \pm \,\infty }}\;$.

What Is Infinity Multiplied By 0

If $f(x)$ approaches $0$ from above, then the limit of $\frac{p(x)}{f(x)}$ is infinity. L’hospital’s rule works great on the two indeterminate forms 0/0 and ${{ \pm \,\infty }}/{{ \pm \,\infty }}\;$. You can usually solve a limit of the form $0 \cdot \infty$ using l'hospital's rule by introducing a fraction. The process of finding the. An indeterminate form is an.

Specifically, If $F(X) \To 0$ And $G(X).

You can usually solve a limit of the form $0 \cdot \infty$ using l'hospital's rule by introducing a fraction. If $f(x)$ approaches $0$ from above, then the limit of $\frac{p(x)}{f(x)}$ is infinity. The process of finding the. An indeterminate form is an expression formed with two of 1, 0, and infinity, and its value cannot be de determined.