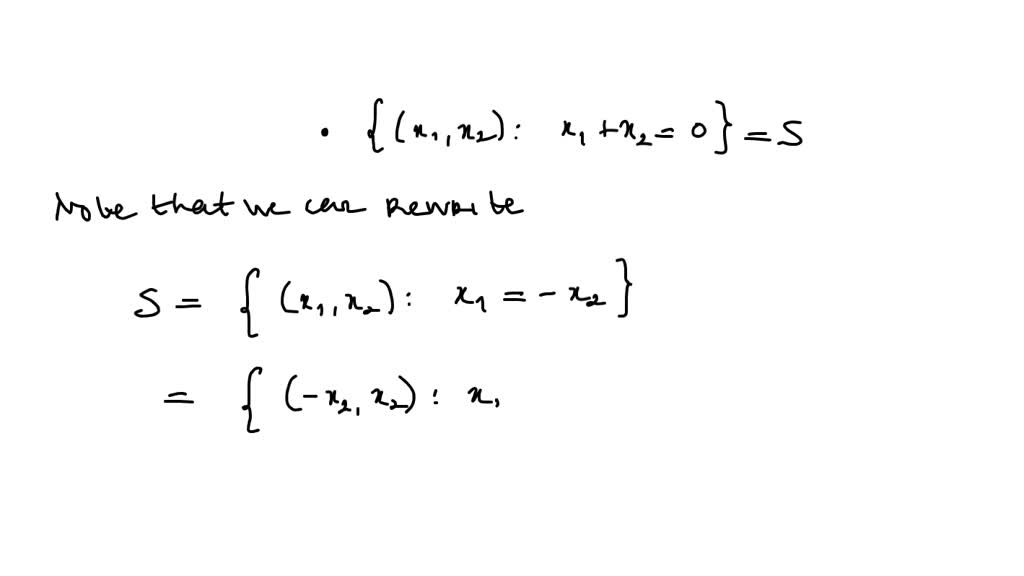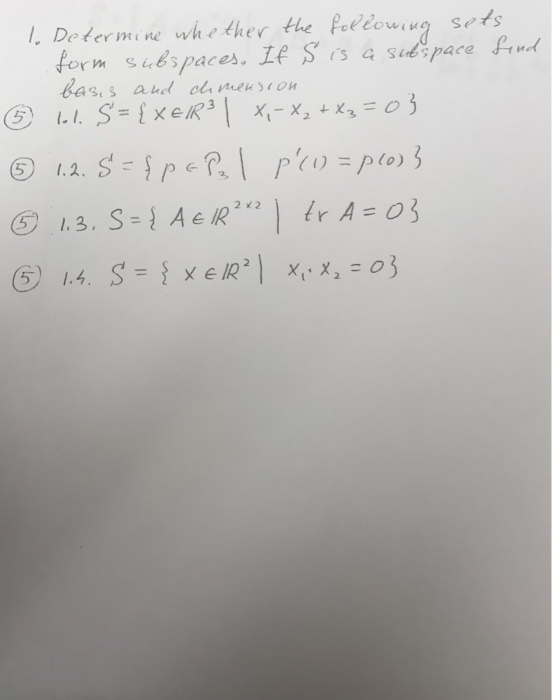Determine Whether The Following Sets Form Subspaces Of R2
Determine Whether The Following Sets Form Subspaces Of R2 - −> subspaces of r2×r2 b. The task is to identify that the given subsets are the subspaces of r 2 or not (a) a = {(x 1, x 2): The set of all 2×2 diagonal matrices. To determine whether the given sets form subspaces of r², each set must be tested for closure under addition and scalar. In mathematics, we can determine whether a set of matrices can serve as subspaces of r2×2 through examining if they satisfy. X 1 + x 2 = 0} checking for the line. Determine whether the following sets form subspaces of r2×r2. To determine whether a set forms a subspace of r2, we need to check if it satisfies three criteria:
To determine whether a set forms a subspace of r2, we need to check if it satisfies three criteria: X 1 + x 2 = 0} checking for the line. −> subspaces of r2×r2 b. Determine whether the following sets form subspaces of r2×r2. The set of all 2×2 diagonal matrices. In mathematics, we can determine whether a set of matrices can serve as subspaces of r2×2 through examining if they satisfy. The task is to identify that the given subsets are the subspaces of r 2 or not (a) a = {(x 1, x 2): To determine whether the given sets form subspaces of r², each set must be tested for closure under addition and scalar.
In mathematics, we can determine whether a set of matrices can serve as subspaces of r2×2 through examining if they satisfy. To determine whether the given sets form subspaces of r², each set must be tested for closure under addition and scalar. To determine whether a set forms a subspace of r2, we need to check if it satisfies three criteria: X 1 + x 2 = 0} checking for the line. −> subspaces of r2×r2 b. Determine whether the following sets form subspaces of r2×r2. The task is to identify that the given subsets are the subspaces of r 2 or not (a) a = {(x 1, x 2): The set of all 2×2 diagonal matrices.
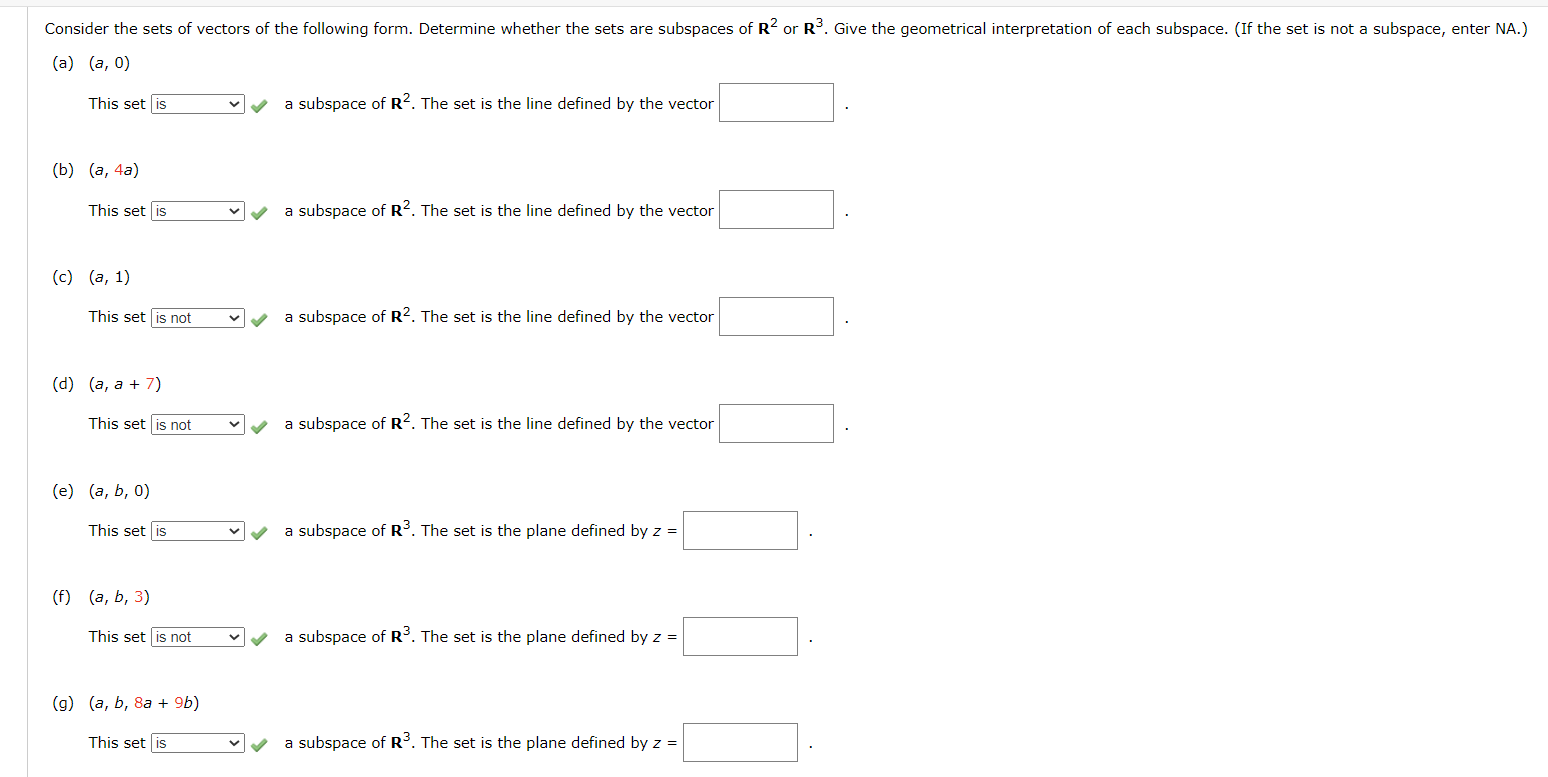
Solved Consider the sets of vectors of the following form.
To determine whether a set forms a subspace of r2, we need to check if it satisfies three criteria: The set of all 2×2 diagonal matrices. In mathematics, we can determine whether a set of matrices can serve as subspaces of r2×2 through examining if they satisfy. To determine whether the given sets form subspaces of r², each set must.
[Solved] Determine whether the following sets form subspaces of R2. (a
To determine whether a set forms a subspace of r2, we need to check if it satisfies three criteria: Determine whether the following sets form subspaces of r2×r2. The task is to identify that the given subsets are the subspaces of r 2 or not (a) a = {(x 1, x 2): In mathematics, we can determine whether a set.
Solved Consider the sets of vectors of the following form.
Determine whether the following sets form subspaces of r2×r2. To determine whether a set forms a subspace of r2, we need to check if it satisfies three criteria: The set of all 2×2 diagonal matrices. X 1 + x 2 = 0} checking for the line. The task is to identify that the given subsets are the subspaces of r.
[Solved] Determine whether the following sets form subspaces of R2. (a
Determine whether the following sets form subspaces of r2×r2. To determine whether the given sets form subspaces of r², each set must be tested for closure under addition and scalar. The task is to identify that the given subsets are the subspaces of r 2 or not (a) a = {(x 1, x 2): The set of all 2×2 diagonal.
SOLVED 1. Determine whether the following sets form subspaces of R? a
X 1 + x 2 = 0} checking for the line. −> subspaces of r2×r2 b. In mathematics, we can determine whether a set of matrices can serve as subspaces of r2×2 through examining if they satisfy. Determine whether the following sets form subspaces of r2×r2. The task is to identify that the given subsets are the subspaces of r.
Solved Consider the sets of vectors of the following form.
In mathematics, we can determine whether a set of matrices can serve as subspaces of r2×2 through examining if they satisfy. The set of all 2×2 diagonal matrices. −> subspaces of r2×r2 b. Determine whether the following sets form subspaces of r2×r2. X 1 + x 2 = 0} checking for the line.
SOLVED Question 13.Determine whether the following sets form subspaces
The set of all 2×2 diagonal matrices. −> subspaces of r2×r2 b. X 1 + x 2 = 0} checking for the line. Determine whether the following sets form subspaces of r2×r2. To determine whether a set forms a subspace of r2, we need to check if it satisfies three criteria:
Solved Determine whether the following sets form subspaces.
Determine whether the following sets form subspaces of r2×r2. −> subspaces of r2×r2 b. The set of all 2×2 diagonal matrices. To determine whether the given sets form subspaces of r², each set must be tested for closure under addition and scalar. To determine whether a set forms a subspace of r2, we need to check if it satisfies three.
[Solved] Determine whether the following sets form subspaces of R2. (a
−> subspaces of r2×r2 b. The task is to identify that the given subsets are the subspaces of r 2 or not (a) a = {(x 1, x 2): X 1 + x 2 = 0} checking for the line. To determine whether the given sets form subspaces of r², each set must be tested for closure under addition and.
Solved 4. (15 points) Determine whether the following sets
−> subspaces of r2×r2 b. Determine whether the following sets form subspaces of r2×r2. The set of all 2×2 diagonal matrices. To determine whether a set forms a subspace of r2, we need to check if it satisfies three criteria: In mathematics, we can determine whether a set of matrices can serve as subspaces of r2×2 through examining if they.
The Set Of All 2×2 Diagonal Matrices.
Determine whether the following sets form subspaces of r2×r2. To determine whether a set forms a subspace of r2, we need to check if it satisfies three criteria: −> subspaces of r2×r2 b. To determine whether the given sets form subspaces of r², each set must be tested for closure under addition and scalar.
The Task Is To Identify That The Given Subsets Are The Subspaces Of R 2 Or Not (A) A = {(X 1, X 2):
X 1 + x 2 = 0} checking for the line. In mathematics, we can determine whether a set of matrices can serve as subspaces of r2×2 through examining if they satisfy.