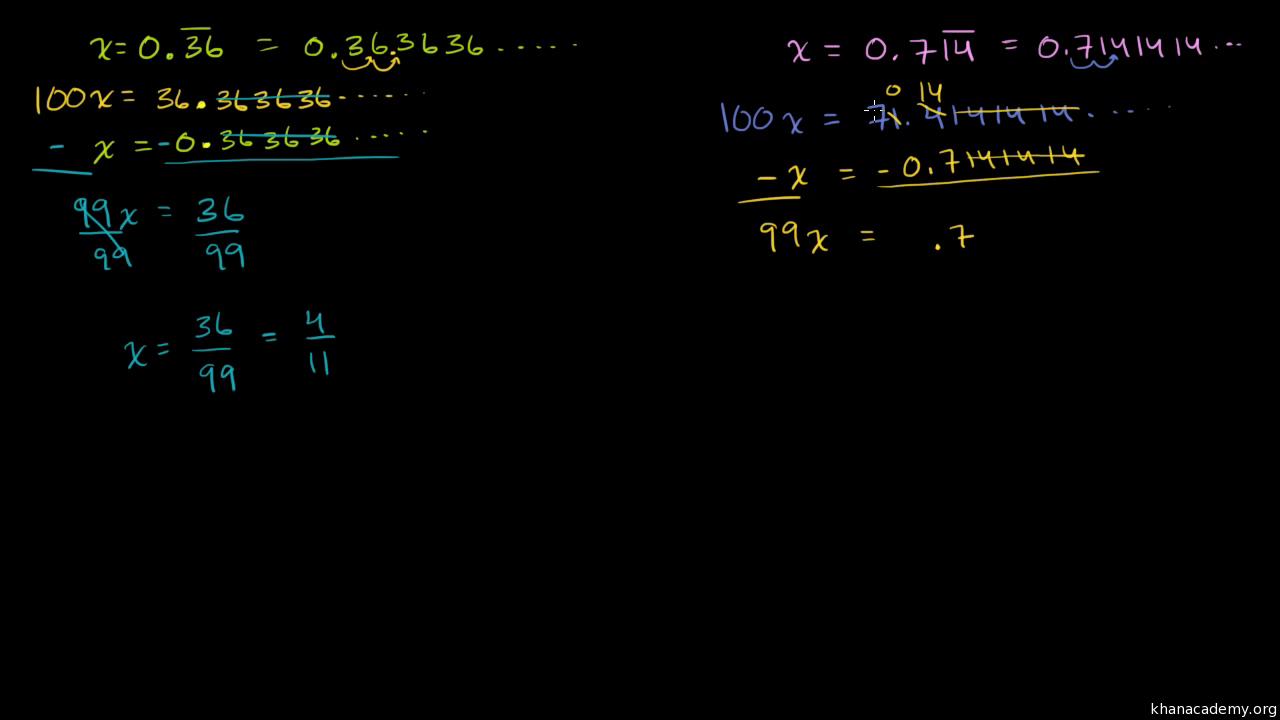What Is 0 83 Repeating As A Fraction
What Is 0 83 Repeating As A Fraction - We first let 0.83 (3 being repeated) be #x#. 0.83 = 56 as the lowest possible fraction. The repeating decimal 0.83 (vinculum notation) has a repeated block length of 1. 0.83 is a repeating decimal number and you want to convert it to a fraction or mixed number. Since x is recurring in 1 decimal places, we multiply it by 10. We first let 0.83 (3 being repeated) be x. Lastly, we divide both sides by 9 to get x as a. When you say 0.83 repeating, you could mean that 3 or 83 is. #10x = 8.33# next, we subtract. Since #x# is recurring in 1 decimal places, we multiply it by 10.
Since #x# is recurring in 1 decimal places, we multiply it by 10. You can use this repeating decimal to fraction conversion calculator to revert a repeating decimal to its original fraction form. 0.83 is a repeating decimal number and you want to convert it to a fraction or mixed number. We first let 0.83 (3 being repeated) be #x#. When you say 0.83 repeating, you could mean that 3 or 83 is. We first let 0.83 (3 being repeated) be x. Since x is recurring in 1 decimal places, we multiply it by 10. 0.83 = 56 as the lowest possible fraction. The repeating decimal 0.83 (vinculum notation) has a repeated block length of 1. Lastly, we divide both sides by 9 to get x as a.
We first let 0.83 (3 being repeated) be x. We first let 0.83 (3 being repeated) be #x#. The repeating decimal 0.83 (vinculum notation) has a repeated block length of 1. Learn how to convert 0.83 repeating to a fraction and understand the concept of repeating decimals as fractions. #10x = 8.33# next, we subtract. When you say 0.83 repeating, you could mean that 3 or 83 is. 0.83 is a repeating decimal number and you want to convert it to a fraction or mixed number. Since #x# is recurring in 1 decimal places, we multiply it by 10. Since x is recurring in 1 decimal places, we multiply it by 10. You can use this repeating decimal to fraction conversion calculator to revert a repeating decimal to its original fraction form.
Repeating Decimal To Fraction Worksheet
Since #x# is recurring in 1 decimal places, we multiply it by 10. 0.83 = 56 as the lowest possible fraction. Lastly, we divide both sides by 9 to get x as a. The repeating decimal 0.83 (vinculum notation) has a repeated block length of 1. Since x is recurring in 1 decimal places, we multiply it by 10.
Repeating Decimal To Fraction Worksheet E Street Light
Since x is recurring in 1 decimal places, we multiply it by 10. Learn how to convert 0.83 repeating to a fraction and understand the concept of repeating decimals as fractions. The repeating decimal 0.83 (vinculum notation) has a repeated block length of 1. You can use this repeating decimal to fraction conversion calculator to revert a repeating decimal to.
Repeating Decimal To Fraction Worksheet E Street Light
0.83 = 56 as the lowest possible fraction. #10x = 8.33# next, we subtract. We first let 0.83 (3 being repeated) be #x#. Since #x# is recurring in 1 decimal places, we multiply it by 10. Since x is recurring in 1 decimal places, we multiply it by 10.
Converting 0.44444 Repeating as a Fraction Solutions and Examples
0.83 is a repeating decimal number and you want to convert it to a fraction or mixed number. Since x is recurring in 1 decimal places, we multiply it by 10. #10x = 8.33# next, we subtract. The repeating decimal 0.83 (vinculum notation) has a repeated block length of 1. When you say 0.83 repeating, you could mean that 3.
Repeating As A Fraction Outlet Stores
#10x = 8.33# next, we subtract. The repeating decimal 0.83 (vinculum notation) has a repeated block length of 1. We first let 0.83 (3 being repeated) be x. You can use this repeating decimal to fraction conversion calculator to revert a repeating decimal to its original fraction form. Learn how to convert 0.83 repeating to a fraction and understand the.
Repeating Decimal To Fraction Worksheet E Street Light
Since x is recurring in 1 decimal places, we multiply it by 10. Lastly, we divide both sides by 9 to get x as a. You can use this repeating decimal to fraction conversion calculator to revert a repeating decimal to its original fraction form. Learn how to convert 0.83 repeating to a fraction and understand the concept of repeating.
Repeating Decimal To Fraction Worksheet E Street Light
Lastly, we divide both sides by 9 to get x as a. Learn how to convert 0.83 repeating to a fraction and understand the concept of repeating decimals as fractions. #10x = 8.33# next, we subtract. You can use this repeating decimal to fraction conversion calculator to revert a repeating decimal to its original fraction form. 0.83 is a repeating.
0.83 as a Fraction Decimal to Fraction
Since x is recurring in 1 decimal places, we multiply it by 10. When you say 0.83 repeating, you could mean that 3 or 83 is. The repeating decimal 0.83 (vinculum notation) has a repeated block length of 1. 0.83 = 56 as the lowest possible fraction. We first let 0.83 (3 being repeated) be x.
Repeating Decimal to Fraction Steps of Conversion, Tricks, Examples
We first let 0.83 (3 being repeated) be x. The repeating decimal 0.83 (vinculum notation) has a repeated block length of 1. Learn how to convert 0.83 repeating to a fraction and understand the concept of repeating decimals as fractions. 0.83 is a repeating decimal number and you want to convert it to a fraction or mixed number. You can.
repeating fraction Decimal Fraction (Mathematics)
Since x is recurring in 1 decimal places, we multiply it by 10. When you say 0.83 repeating, you could mean that 3 or 83 is. We first let 0.83 (3 being repeated) be x. 0.83 is a repeating decimal number and you want to convert it to a fraction or mixed number. #10x = 8.33# next, we subtract.
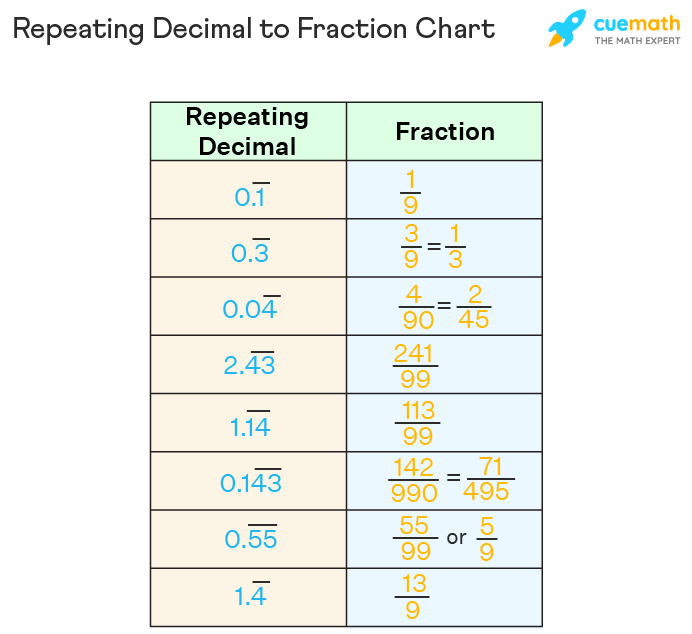
You Can Use This Repeating Decimal To Fraction Conversion Calculator To Revert A Repeating Decimal To Its Original Fraction Form.
#10x = 8.33# next, we subtract. The repeating decimal 0.83 (vinculum notation) has a repeated block length of 1. 0.83 is a repeating decimal number and you want to convert it to a fraction or mixed number. Learn how to convert 0.83 repeating to a fraction and understand the concept of repeating decimals as fractions.
Since X Is Recurring In 1 Decimal Places, We Multiply It By 10.
We first let 0.83 (3 being repeated) be #x#. Lastly, we divide both sides by 9 to get x as a. Since #x# is recurring in 1 decimal places, we multiply it by 10. 0.83 = 56 as the lowest possible fraction.
We First Let 0.83 (3 Being Repeated) Be X.
When you say 0.83 repeating, you could mean that 3 or 83 is.