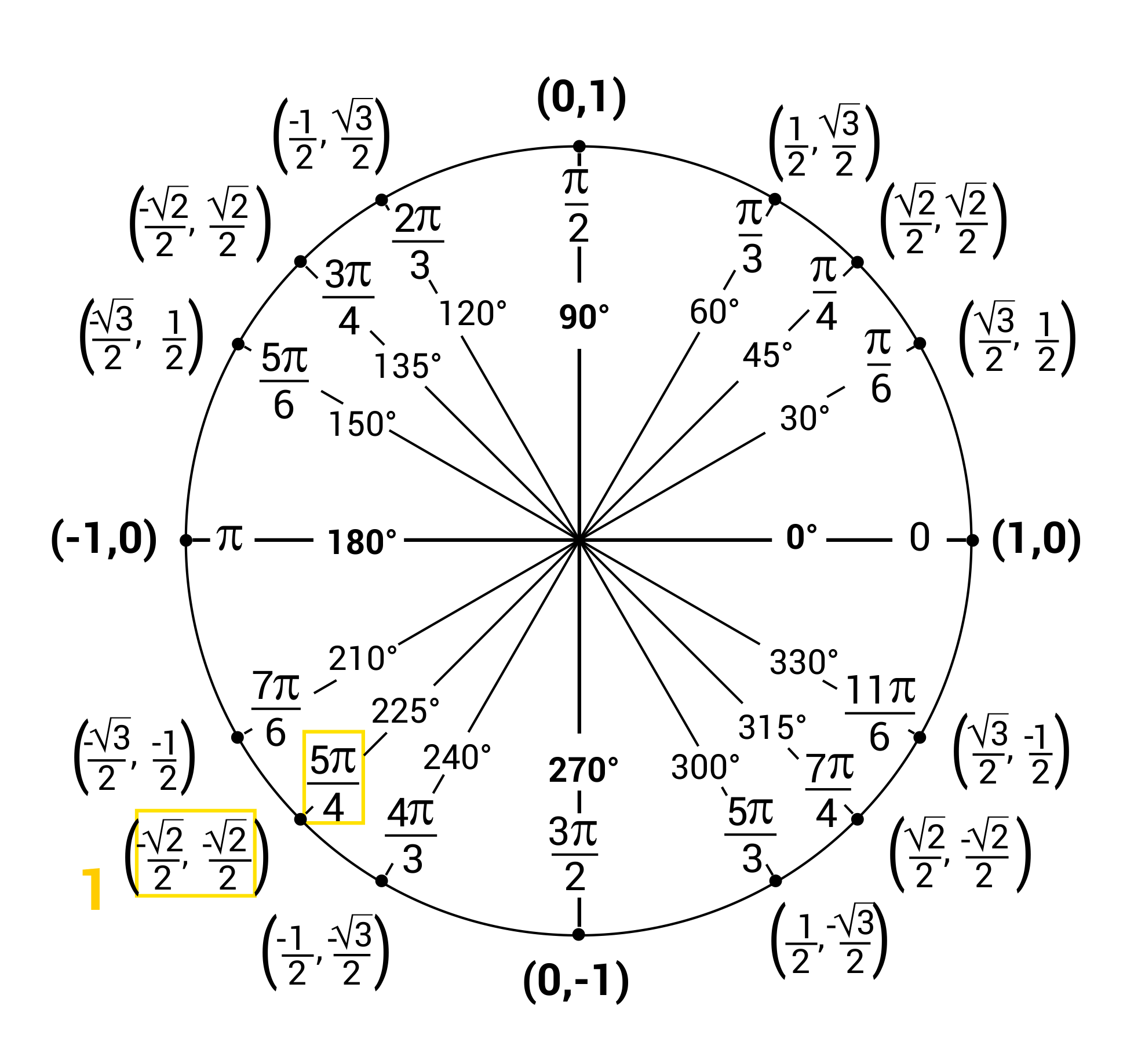
What Is The Reference Angle For 5Pi 3
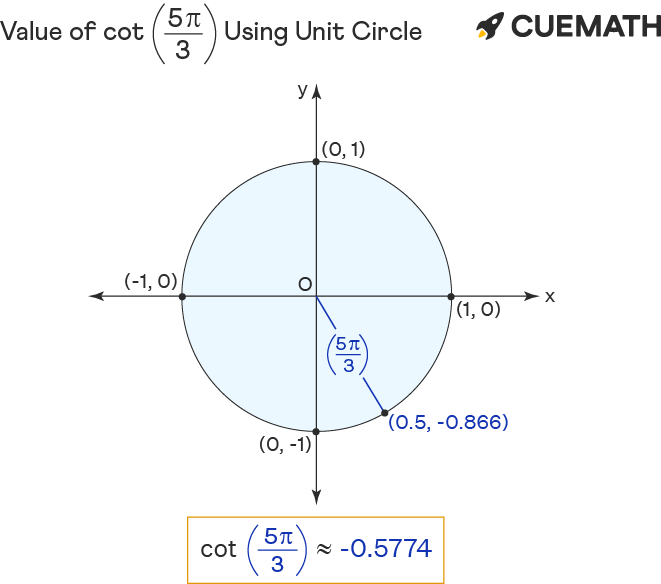
What Is The Reference Angle For 5Pi 3 - The reference angle for 5π/3 is π/3. The angle is, ⇒ 5π / 3. Therefore the correct option is b. Given, angle in radians = 5π/3. The reference angle of 3π/4 will be π/3. Since 5π/3 radians is more than π (180°), it is located in the fourth quadrant of the unit. The latter is known as the vertex of the angle and the rays as the sides, sometimes as the legs and sometimes the arms of the angle. Here, we can clearly see that. To find the reference angle for 5π/3, we need to determine the equivalent angle within one full. The angle 5pi/3 is in the fourth quadrant (meaning cosine is positive while sine & tangent are negative), and its reference angle is 60 degrees with respect to the horizontal.
Given, angle in radians = 5π/3. The angle is, ⇒ 5π / 3. Here, we can clearly see that. The latter is known as the vertex of the angle and the rays as the sides, sometimes as the legs and sometimes the arms of the angle. The angle 5pi/3 is in the fourth quadrant (meaning cosine is positive while sine & tangent are negative), and its reference angle is 60 degrees with respect to the horizontal. The reference angle of 3π/4 will be π/3. The reference angle for 5π/3 is π/3. Therefore the correct option is b. To find the reference angle for 5π/3, we need to determine the equivalent angle within one full. Since 5π/3 radians is more than π (180°), it is located in the fourth quadrant of the unit.
The angle is, ⇒ 5π / 3. The latter is known as the vertex of the angle and the rays as the sides, sometimes as the legs and sometimes the arms of the angle. The reference angle of 3π/4 will be π/3. The reference angle for 5π/3 is π/3. The angle 5pi/3 is in the fourth quadrant (meaning cosine is positive while sine & tangent are negative), and its reference angle is 60 degrees with respect to the horizontal. To find the reference angle for 5π/3, we need to determine the equivalent angle within one full. Here, we can clearly see that. Since 5π/3 radians is more than π (180°), it is located in the fourth quadrant of the unit. Given, angle in radians = 5π/3. Therefore the correct option is b.
Unit Circle Practice Worksheets
The reference angle of 3π/4 will be π/3. To find the reference angle for 5π/3, we need to determine the equivalent angle within one full. Given, angle in radians = 5π/3. The angle is, ⇒ 5π / 3. The latter is known as the vertex of the angle and the rays as the sides, sometimes as the legs and sometimes.
The reference angle for (5pi)/4 is pi/4 , which has a terminal point of
The reference angle for 5π/3 is π/3. The angle 5pi/3 is in the fourth quadrant (meaning cosine is positive while sine & tangent are negative), and its reference angle is 60 degrees with respect to the horizontal. Since 5π/3 radians is more than π (180°), it is located in the fourth quadrant of the unit. The reference angle of 3π/4.
inverse trigonometric functions and reference angles for the following
The angle is, ⇒ 5π / 3. The reference angle of 3π/4 will be π/3. The reference angle for 5π/3 is π/3. Here, we can clearly see that. To find the reference angle for 5π/3, we need to determine the equivalent angle within one full.
Reference Angles NBKomputer
To find the reference angle for 5π/3, we need to determine the equivalent angle within one full. Since 5π/3 radians is more than π (180°), it is located in the fourth quadrant of the unit. The reference angle for 5π/3 is π/3. The angle is, ⇒ 5π / 3. Therefore the correct option is b.
Cot 5pi/3 Find Value of Cot 5pi/3 Cot 5π/3
The angle is, ⇒ 5π / 3. Therefore the correct option is b. The latter is known as the vertex of the angle and the rays as the sides, sometimes as the legs and sometimes the arms of the angle. Here, we can clearly see that. The reference angle of 3π/4 will be π/3.
Angle Of Rotation Examples
Here, we can clearly see that. Since 5π/3 radians is more than π (180°), it is located in the fourth quadrant of the unit. Therefore the correct option is b. The reference angle of 3π/4 will be π/3. The latter is known as the vertex of the angle and the rays as the sides, sometimes as the legs and sometimes.
pi/3 is the reference angle for A. 2pi/3 B. 15pi/3 C. 7pi/3 D. 19pi/3
The angle 5pi/3 is in the fourth quadrant (meaning cosine is positive while sine & tangent are negative), and its reference angle is 60 degrees with respect to the horizontal. Since 5π/3 radians is more than π (180°), it is located in the fourth quadrant of the unit. Given, angle in radians = 5π/3. The latter is known as the.
for this special angle, draw the angle and find the reference angle t
The angle is, ⇒ 5π / 3. The angle 5pi/3 is in the fourth quadrant (meaning cosine is positive while sine & tangent are negative), and its reference angle is 60 degrees with respect to the horizontal. Therefore the correct option is b. The reference angle of 3π/4 will be π/3. Here, we can clearly see that.
What is the reference angle and cosine of StartFraction 7 pi Over 6
Therefore the correct option is b. Here, we can clearly see that. To find the reference angle for 5π/3, we need to determine the equivalent angle within one full. Since 5π/3 radians is more than π (180°), it is located in the fourth quadrant of the unit. The angle is, ⇒ 5π / 3.
Ex Sine And Cosine Values Using The Unit Circle Multiples, 54 OFF
Given, angle in radians = 5π/3. The angle is, ⇒ 5π / 3. To find the reference angle for 5π/3, we need to determine the equivalent angle within one full. The reference angle of 3π/4 will be π/3. The latter is known as the vertex of the angle and the rays as the sides, sometimes as the legs and sometimes.
Since 5Π/3 Radians Is More Than Π (180°), It Is Located In The Fourth Quadrant Of The Unit.
The angle 5pi/3 is in the fourth quadrant (meaning cosine is positive while sine & tangent are negative), and its reference angle is 60 degrees with respect to the horizontal. Here, we can clearly see that. Therefore the correct option is b. The angle is, ⇒ 5π / 3.
Given, Angle In Radians = 5Π/3.
The reference angle of 3π/4 will be π/3. To find the reference angle for 5π/3, we need to determine the equivalent angle within one full. The latter is known as the vertex of the angle and the rays as the sides, sometimes as the legs and sometimes the arms of the angle. The reference angle for 5π/3 is π/3.