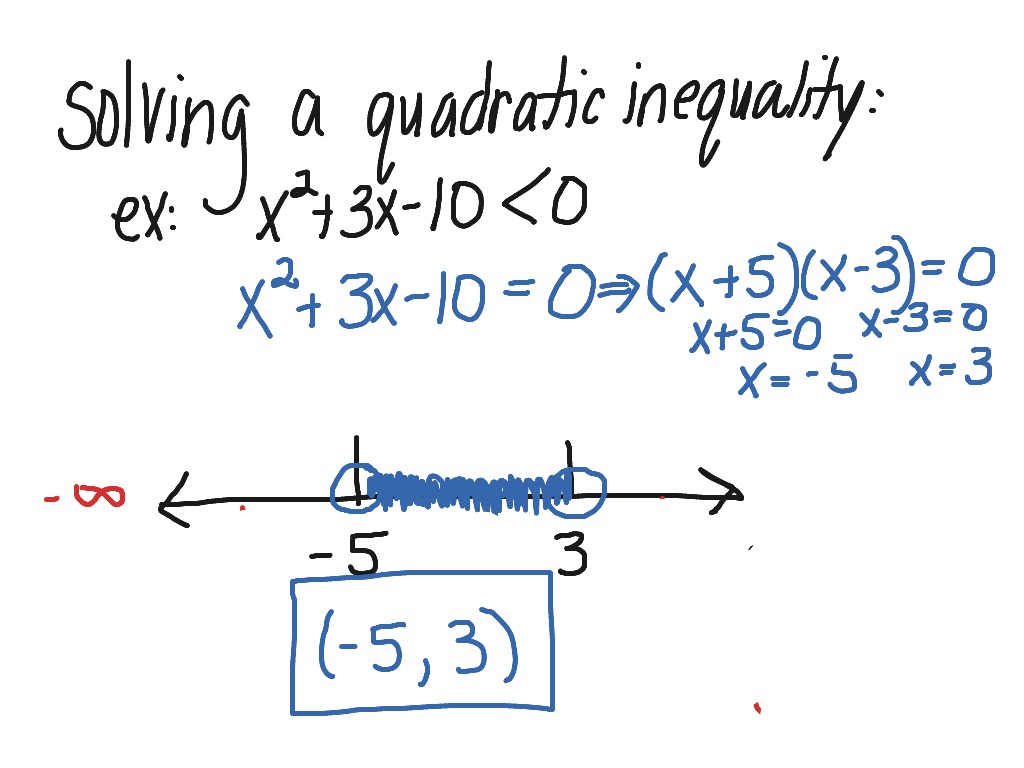What Is The Solution Set Of The Quadratic Inequality Mc010 1 Jpg
What Is The Solution Set Of The Quadratic Inequality Mc010 1 Jpg - To solve a quadratic inequality, follow these steps: Find the solution set of the quadratic inequality x 2 + 2 x − 8 > 0 without graphing. A ∈ ℜ, b ∈ ℜn and c ∈ ℜ. Let c ⊆ ℜn be the solution set of a quadrtatic inequality, c = {x ∈ ℜn | xtax + btx + c ≤ 0}. Arrange the terms so that one side of the inequality is equal to 0, i.e., a x 2 + b x +. To find the solution set without graphing, first.
To solve a quadratic inequality, follow these steps: Find the solution set of the quadratic inequality x 2 + 2 x − 8 > 0 without graphing. A ∈ ℜ, b ∈ ℜn and c ∈ ℜ. Let c ⊆ ℜn be the solution set of a quadrtatic inequality, c = {x ∈ ℜn | xtax + btx + c ≤ 0}. To find the solution set without graphing, first. Arrange the terms so that one side of the inequality is equal to 0, i.e., a x 2 + b x +.
A ∈ ℜ, b ∈ ℜn and c ∈ ℜ. To solve a quadratic inequality, follow these steps: To find the solution set without graphing, first. Arrange the terms so that one side of the inequality is equal to 0, i.e., a x 2 + b x +. Find the solution set of the quadratic inequality x 2 + 2 x − 8 > 0 without graphing. Let c ⊆ ℜn be the solution set of a quadrtatic inequality, c = {x ∈ ℜn | xtax + btx + c ≤ 0}.
Solved Which quadratic inequality does the graph below represent
A ∈ ℜ, b ∈ ℜn and c ∈ ℜ. To find the solution set without graphing, first. Let c ⊆ ℜn be the solution set of a quadrtatic inequality, c = {x ∈ ℜn | xtax + btx + c ≤ 0}. Arrange the terms so that one side of the inequality is equal to 0, i.e., a x.
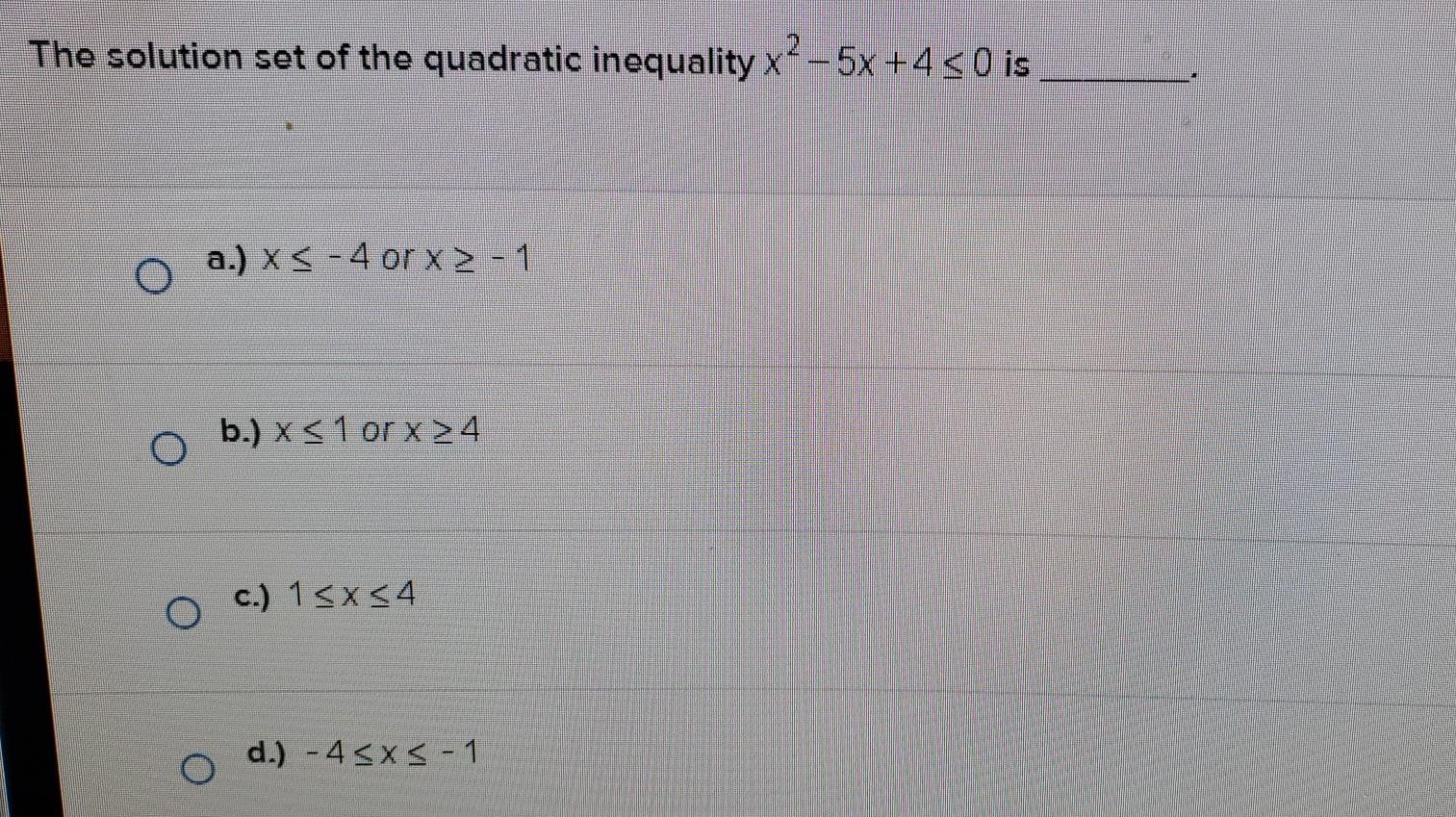
Solved Identify the solution set of the quadratic inequality
Let c ⊆ ℜn be the solution set of a quadrtatic inequality, c = {x ∈ ℜn | xtax + btx + c ≤ 0}. A ∈ ℜ, b ∈ ℜn and c ∈ ℜ. To find the solution set without graphing, first. Arrange the terms so that one side of the inequality is equal to 0, i.e., a x.
Solving A Quadratic Inequality Algebraically
Arrange the terms so that one side of the inequality is equal to 0, i.e., a x 2 + b x +. A ∈ ℜ, b ∈ ℜn and c ∈ ℜ. To find the solution set without graphing, first. To solve a quadratic inequality, follow these steps: Find the solution set of the quadratic inequality x 2 + 2.
Give an example of a quadratic inequality whose solution set is the
To solve a quadratic inequality, follow these steps: Let c ⊆ ℜn be the solution set of a quadrtatic inequality, c = {x ∈ ℜn | xtax + btx + c ≤ 0}. To find the solution set without graphing, first. A ∈ ℜ, b ∈ ℜn and c ∈ ℜ. Find the solution set of the quadratic inequality x.
Solving Quadratic Inequalities
Arrange the terms so that one side of the inequality is equal to 0, i.e., a x 2 + b x +. Find the solution set of the quadratic inequality x 2 + 2 x − 8 > 0 without graphing. Let c ⊆ ℜn be the solution set of a quadrtatic inequality, c = {x ∈ ℜn | xtax.
Solved Task 2 (quadratic inequality) Find the solution set for the
To solve a quadratic inequality, follow these steps: Find the solution set of the quadratic inequality x 2 + 2 x − 8 > 0 without graphing. Arrange the terms so that one side of the inequality is equal to 0, i.e., a x 2 + b x +. A ∈ ℜ, b ∈ ℜn and c ∈ ℜ. To.
[ANSWERED] Solve the quadratic inequality Give the solution set
To solve a quadratic inequality, follow these steps: A ∈ ℜ, b ∈ ℜn and c ∈ ℜ. Arrange the terms so that one side of the inequality is equal to 0, i.e., a x 2 + b x +. Find the solution set of the quadratic inequality x 2 + 2 x − 8 > 0 without graphing. Let.
Which graph represents the solution set for the quadratic inequality x2
Arrange the terms so that one side of the inequality is equal to 0, i.e., a x 2 + b x +. To solve a quadratic inequality, follow these steps: Find the solution set of the quadratic inequality x 2 + 2 x − 8 > 0 without graphing. A ∈ ℜ, b ∈ ℜn and c ∈ ℜ. To.
Quadratic Equation Inequalities Tessshebaylo
Let c ⊆ ℜn be the solution set of a quadrtatic inequality, c = {x ∈ ℜn | xtax + btx + c ≤ 0}. Arrange the terms so that one side of the inequality is equal to 0, i.e., a x 2 + b x +. To solve a quadratic inequality, follow these steps: Find the solution set of.
To Solve A Quadratic Inequality, Follow These Steps:
Find the solution set of the quadratic inequality x 2 + 2 x − 8 > 0 without graphing. To find the solution set without graphing, first. Arrange the terms so that one side of the inequality is equal to 0, i.e., a x 2 + b x +. Let c ⊆ ℜn be the solution set of a quadrtatic inequality, c = {x ∈ ℜn | xtax + btx + c ≤ 0}.
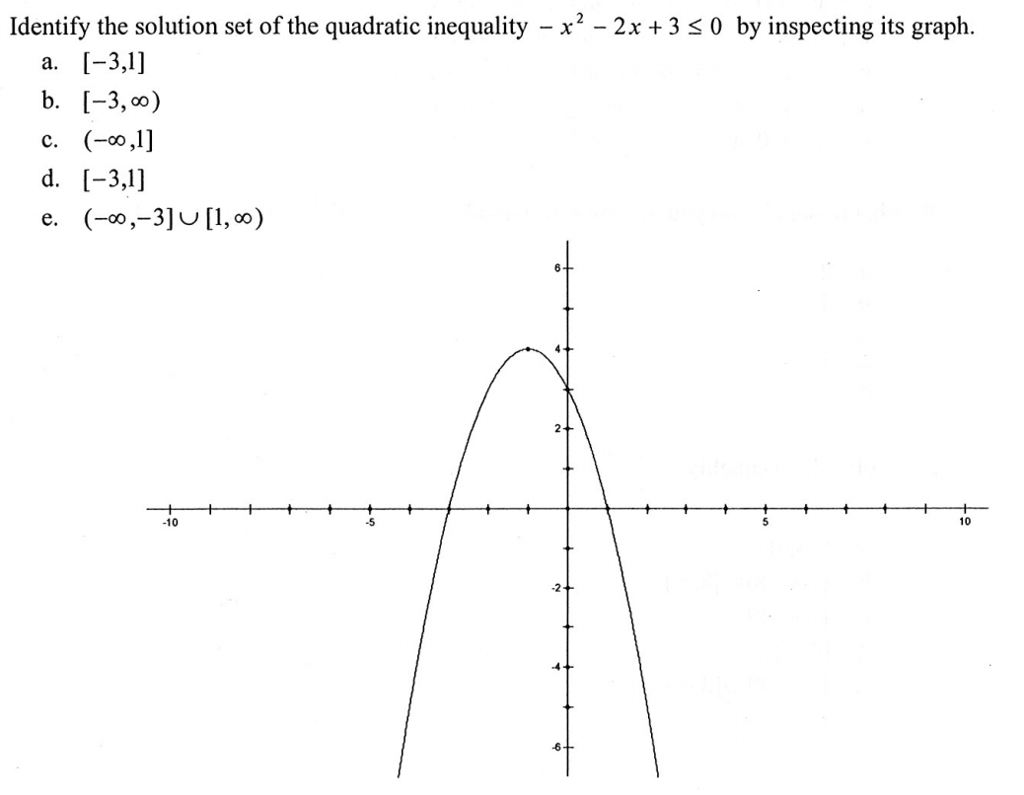



![[ANSWERED] Solve the quadratic inequality Give the solution set](https://media.kunduz.com/media/sug-question-candidate/20231028232951207856-5934294.jpg?h=512)